Ivan Lovrenović

Uvod (I. Lovrenović)

Dr. fra Mijo (Vitomir) Bobetić, rođen 1921. godine u Livnu , umro 1998. u Montrealu (Kanada), bio je franjevac, član Provincije Bosne Srebrene, i vrhunski znanstvenik - fizičar i matematičar. Šturi leksikonski podaci o njemu govore da je završio studij teologije na Franjevačkoj teo­logiji u Sarajevu 1946, a fizike na Prirodoslovno-matematičkom fakultetu u Zagrebu 1953. Službovao je kao svećenik od 1946. do 1949. u Gorici kraj Livna, u Kreševu, Kiseljaku i Zenici. U Franjevačkoj gimnaziji u Visokome bio je profesor matematike i fizike od 1954. do 1960. Nakon kraćeg boravka u Njemačkoj otišao je 1961. u Ameriku. Bio je asistent dvostrukog nobelovca Johna Bardeena na Sveučilištu Illinois u Urbani te je 1961-63. radio na problemu apsorpcije ultrazvuka od supravodiča. Od 1965. profesor je matematike na Regina Mundi Collegeu u Londonu (Kanada, država Ontario), zatim asistent na Odsjeku za primije­njenu matematiku na Sveučilištu u Waterloou, Quebec 1967-70, gdje je 1971. doktorirao iz primijenjene matematike temom Interatomic Forces and the Properties of Crystallin Inert Gases: Argon, Krypton. Uz novčanu pomoć kanadske vlade obavljao je 1970. i 1975. istraživanja u IBM Research Laboratory for Large Scale Computa­tions u San Joseu (Kalifornija). Od 1971. do 1974. asistent je na Loyola Collegeu, a potom izvan­redni profesor na Concordia University u Montrealu. Istražuje multiparametarske intermolekularne funk­cije svijetlih plinova. Rezultate istraživanja objavio je na engleskom jeziku u publikacijama Physical Reviev (New York 1964, 1970-72, 1983), Journal of Physics (London 1971), Molecular Physics (London 1971), Phy­sics Letters (Amsterdam 1971), Journal of Chemical Physics (New York 1976, 1983), Journal of Research and Development (Birmingham 1976).  Član je American Association for Advancement of Science, a od 1980. aktivni član New York Academy of Sciences. Studiju o Ruđeru Boškoviću objavio je u Hrvatskoj reviji (München), u Studia Croatica (Buenos Aires) i u franjevačkom časopisu Nova et vetera (Sarajevo).

Franjevačka bilješka o fra Miji Bobetiću kaže: „O svojim znanstve­nim dostignućima nije govorio te je za njih znalo vrlo malo članova njegove franjevačke provincije.“

***

Fra Mijo Bobetić, makar dalek i neprisutan, bio mi je važna figura u odrastanju. O njemu se pričalo mnogo i često (u obitelji su ga zvali rođenim imenom: Vito), a viđali smo ga rijetko kad bi nakratko banuo („k'o vitar!“), pun neobičnih šala. Đaci franjevačke gimnazije u Visokome, kojima je predavao fiziku i matematiku, pamtili su ga kao vrlo strogog i naopakog. Mojima je od njega redovito za Božić stizala čestitka u kuverti, i uz nju po stotinu kanadskih dolara.

U knjizi Sedam dana po Bosni u kolovozu 2008. zabilježio sam jedno sjećanje na fra Miju Bobetića, našega Vitu:

...Ista ova cesta, samo davno prije asfalta, bijela od prašine, sjedim uz majku na fijakerskom sjedalu, dok fra Mijo Bobetić, rođak i prijatelj, drži kajase zbijajući šale sa mnom. Vozimo se u Čuklić „na ljetovanje“, tamo je fra Mijina mati, legendarna tetka Ruža, babina sestra, domaćica kod staroga fra Luje Franjičevića. Tih mjesec dana pod Kamešnicom svijetle u sjećanju poput žar-ptice iz bajke. U starinskom drvenom zahodu prvi put sam se susreo, oči u oči, sa strašnim stvorom škorpijom, pod nepcima i sad mogu oživjeti okus i hrskanje ušećerenog meda tetke Ruže, momak što se brinuo oko jednoga konja i krave u štali učio me kako se zahvaća voda iz čatrnje nasred velikoga dvorišta kantom vezanom na dugi konopac. Volio sam se bacati i valjati po njegovoj širokoj postelji od slame u suhom dijelu štale pa sam mu slomio ogledalce što ga je držao pod stroškom, i danas se sjećam srama i kajanja koje me progonilo kad sam vidio koliko je tužan zbog toga.

Vrhunski matematičar, zanesen naukom i posvećen njoj, fra Mijo Bobetić je kasnije napustio gimnaziju u Visokome, na svoju ruku i na vlastiti rizik otišao prvo u Njemačku potom u Ameriku i Kanadu, gdje je postao eminentan autor iz nekih usko specijalističkih matematičkih istraživanja. Do papske je stolice morala ići njegova molba da mu se odobri status. Samo je on znao kroza što je morao proći, nakon što se iskrcao u njujorškoj luci sa stotinu dolara u džepu. Za jednoga ljetnog dolaska u domovinu, kada je već bio priznat znanstvenik, pričao nam je o tom svom prvom susretu s Amerikom. Trebalo se najprije pobrinuti za neku početnu zaradu, bilo kakvu. Kupio sam, kaže, one njihove novine od kilograma, a sve oglasi, sjednem u park na klupu, te listaj, listaj. Naiđem na oglas u kojem neki bogataš traži tko bi mu prevezao njegov cadillac s istočne na zapadnu obalu, iz New Yorka u San Francisco; za to bi dobio dobru plaću, putne troškove i povratnu avionsku kartu. Javim se, i čovjek me zaposli. Putovao sam mjesec dana, jer je jedan od uvjeta bio da ne vozim prebrzo, da se auto ne ošteti. Mnogo mi je valjao taj put, jer nikada ne bih tako upoznao Ameriku.

S krajnjom dosljednošću njegovao je Bobetić potpunu anonimnost u našem dijelu svijeta, kao i u hrvatskoj dijaspori u Kanadi i Americi, mareći samo za obitelj. Pisao sam mu u vrijeme kada sam pripremao knjigu proze o bosanskim franjevcima suočenima kroz historiju s izazovima „vanjskoga svijeta“, imajući u vidu i njegovo iskustvo. Odgovorio  mi je gotovo panično: ne, nemoj mene, nemoj mene nipošto, moje iskustvo ništa ti ne može značiti... Objavio je tek jedanput, 1980. godine, autorski članak u sarajevskom franjevačkom časopisu Nova et vetera o Ruđeru Boškoviću kao osnivaču modernoga atomizma, demonstrirajući znanje i diskurs sasvim rijedak u tadašnjoj našoj intelektualnoj produkciji. Umro je i pokopan u Montrealu, i osim obitelji i starijih fratara, vjerojatno ga se sjećaju samo u nekim najužim matematičarskim krugovima. 

Dr. fra Mijo V. Bobetić, Ruđer Josip Bošković - osnivač modernog atomizma

Nova et vetera, godina XXX, svezak 2, Sarajevo 1980.

Jedan od rijetko suptilnih i vizionarskih znanstvenika i mislilaca, koje je hrvatski narod dao evropskoj kulturnoj baštini, bio je Ruđer Josip Bošković, svećenik, član isusovačkog reda, u svoje vrijeme poznat kao filozof, fizičar, matematičar, astronom, geodet, arhitekt, pjesnik i diplomat, a u moderno doba kao atomist.[1] Ono što je Boškovića učinilo privlačnim modernim učenjacima, jest činjenica, da je on prvi dao prih­vatljive misli o prirodi atomskih čestica kao i o interakciji molekularnih sila. Njegov utjecaj na Faradaya, a preko njega i na C. Maxwella, bez sumnje je ostavio vidnog traga u razvoju fizike 19. stoljeća. Široj suvremenoj javnosti postao je poznat nakon dvojezičnog (latinsko-engleskog) izdanja njegove Teorije u Londonu, 1922, s predgovorom prevo­dioca J. M. Childa i kratkim životopisom B. Petronijevića.[2]

Boškovićeve ideje su općenito naišle na pozitivnu ocjenu u ondaš­njim naučnim krugovima. Posebno je bio cijenjen u Engleskoj i Francus­koj, mada je imao i žestokih protivnika. Objavio je preko stotinu, što knjiga, što članaka, za koje francuski astronom de Lalande kaže: „u svakoj od njih ima ideja dostojnih jednog genija“.[3] I zaista, kad čovjek čita njegovu Teoriju prirodne filozofije ostaje zadivljen s kolikom je ispravnošću svojih ideja, kvalitativnim procjenama, kao i dubokom na­učnom intuicijom bio skoro 200 godina ispred svojih suvremenika. Nije čudo, da L. L. Whyte kaže za njega: „A twentieth-century mind in the eighteenth Century“[4] - mozak 20. stoljeća u 18. stoljeću.

U ovoj kratkoj studiji namjera mi je da iznesem nekoliko važnijih biografskih podataka, kao i za modernu nauku njegove najvažnije znanstvene misli. Inače, njegov rad je bico toliko raznovrstan i opsežan, gotovo uvijek pisan elegantnim latinskim jezikom, često puta u stihovima, a njegov život nemiran i buran, da još uvijek predstavlja izazovi za moder­nog biografa. Knjiga Ruđer Bošković, od Dr. Ž. Markovića, u dva sveska s ukupno oko 1200 stranica, odlično je uspio pokušaj, da se osvi­jetli lik tog naučnog velikana te može poslužiti kao bogat izvor podataka o njegovu životu, ličnosti i radu.[5]

I.

Ruđer Josip Bošković potječe iz brojne obitelji Nikole Bošković i Pavice rod. Bettera, kćeri dubrovačkog trgovca i pjesnika Bartolomeja Bettera. Rođen je u Dubrovniku 18. svibnja 1711. Starinom, Ruderova obitelj potječe iz Orahova u današnjoj Hercegovini, mada postoji i mi­šljenje, da je to Orahov Dol koji je bio u sklopu Dubrovačke republike. Danas on pripada rimokatoličkoj župi Ravno, Hercegovina, a udaljen je kojih 16 km od priobalskog, turističkog mjesta Slano. Dalmatinci ga nazivaju Orahovo, a sami mještani Orahov Dol. Tu još uvijek stoji kuća Boškovića - istina prerađivana i popravljana - i danas nastanjena od hrvatske katoličke porodice Tomičić. Po predaji same porodice smatra se, da je to u stvari porodica Bošković s promijenjenim prezimenom. Ma koja verzija bila ispravna, u matici krštenih, koja se čuva u dubro­vačkom arhivu, stoji da je osmo dijete Nikole i Pavice Bošković, Ruđer Josip, kršten u rimokatoličkoj vjeri 26. svibnja 1711. Nikola Bošković, kao sudionik dubrovačkog trgovca Rade Gleđevića, proveo je neko vri­jeme u Novom Pazaru u Srbiji, odakle je Dubrovačka republika, kao i druge zapadne zemlje, podržavala trgovačke veze s Bizantom. Međutim, u austro-turskom ratu grad je bio uništen, pa izgubivši dobar dio imo­vine, Nikola se povratio u Dubrovnik, gdje je umro, kad je Ruđeru bilo 10 godina. Pavica, Ruđerova majka, doživjela je duboku starost od 103 godine.

Ruđer je bio oduševljen svojim gradom i ponosio se njim cijelog života. U njemu je proveo svoje djetinjstvo, prvih 14 godina, i volio ga kao svoju rođenu grudu. U svojoj pjesmi „O pomrčinama Sunca i Mje­seca“ piše: „Slavljeni po cijelom svijetu, slatki moj zavičaj Dubrovnik, diči se odličnim djedovima i pradjedovima“.

Mladi Ruđer, kao i sva ostala njegova braća, pohađao je školu u dubrovačkom Isusovačkom kolegiju, gdje je odmah zapažen kao talen­tiran student. Tu je stekao osnove latinskog jezika, u kome se poslije posebno odlikovao klasičnom elegancijom stila. Dubrovnik s najbližom okolicom, obdaren neuporedivim prirodnim ljepotama, bio je u to vri­jeme slobodna republika te kulturni i trgovački centar na Jadranskoj obali, nazvan hrvatskom Atenom. Te prirodne ljepote kao i stoljetna kulturna ostavština, nije izmakla Ruđerovom bistrom oku, osjetljivoj, ponosnoj i pjesnički nastrojenoj prirodi. Kao mladić, oduševljavao se Marinom Getaldićem, poznatim dubrovačkim matematičarom 16. sto­ljeća.[6]

Godine 1725. poslan je u Rim na poznati isusovački Collegium Romanum na više obrazovanje. Poslije dvije godine novicijata, nastavlja studij na toj ustanovi, najprije retoriku i poetiku a onda filozofiju, matematiku i fiziku. Odmah je zapažena njegova velika nadarenost i sklonost za matematiku, fiziku i astronomiju. Bošković je bio prvi koji je u Italiji branio Newtonove ideje.

Već 1733. počeo je predavati matematiku, fiziku i astronomiju na nižim odgojnim zavodima Reda. Za svećenika je zaređen 1740. godine. U to vrijeme počinje i s prvim publikacijama iz primijenjene matema­tike, mehanike, geodezije, geofizike i astronomije. Njegova vlastita istra­živanja na području nauke, kao i ljubav prema mladima napravila je od njega izvrsnog predavača. Pokazao je veliki elan i gotovo neiscrpivu energiju.

U početku svoje znanstvene karijere, Bošković je posvetio posebnu pažnju i ljubav prema astronomiji. Već godine 1736. objavio je svoj prvi rad: De Maculis Solaribus — O sunčanim pjegama — u kojem su njegova vlastita zapažanja i zaključci bili od neprocjenjive vrijednosti za tu još i danas zagonetnu prirodnu pojavu. Duboko u noć provodio je vrijeme promatrajući svemir, posebno planete i komete Sunčanog sustava. Iz tog razdoblja potječu i njegove publikacije: Rasprava o najnovijem prolazu Merkura ispred Sunca, Rasprava o polarnoj svjetlosti, Rasprava o novoj upotrebi dalekozora za promatranje nebeskih objekata. Predložio je nacrt efikasnijeg mikrometra od onog u dotadašnjoj upotrebi. U isto vrijeme radio je i na problemima sferne trigonometrije. Dao je sva osnovna rješenja te grane matematike i smatra se njenim definitivnim osnivačem.

Bošković, izgleda, nije pridavao veću pažnju višoj matematičkoj analizi, koju su započeli Newton i Leibniz a posebno je njegovali fran­cuski matematičari. „Infinitezimalni procesi“ kao i „infinitezimalne veli­čine“ za Boškovića nisu bili jasno definirani. On kaže da njihovi autori ispunjavaju cijele stranice mučnim izvodima, koje nitko ne čita i ne trudi se da ih shvati u cijelosti. Istina, on se služio metodama besko­načno malih veličina; o tome je napisao i raspravu: O Prirodi i upotre­bi beskonačno velikih i beskonačno malih veličina. Međutim, njegove metode bile su geometrijske i grafičke, dakle zorne, pomoću kojih je, zaobilazeći teške izvode više analize, postizavao svoje rezultate. Ipak, upozoravao je na opasnost bezobzirne manipulacije tim veličinama, jer u njihovim osnovama leži ideja djeljivosti prostora u beskonačnost. U geometriji je otišao tako daleko, da je čak razmatrao mogućnost struk­ture neeuklidske geometrije, koju su kasnije dublje razvili J. Bolyai, Lobačevski i Gauss. Bilo je jasno da se njegov praktički duh sve više okretao pirema pozitivnim znanostima, radije nego prema teologiji i skolastičkoj filozofiji.

Godine 1743. bio je izabran od pape Benedikta XIV. za tehničkog savjetnika u Papinoj državi. U tom svojstvu bilo mu je povjereno, da sa još dvojicom stručnjaka podnese izvještaj o tome, što bi trebalo učiniti da se pukotine, koje su se pojavile na Michelangelovoj kupoli crkve sv. Petra u Rimu, poprave i kako da se spriječi daljni kvar. Boško­vićev izvještaj i sugestije bile su prihvaćene u cijelosti: kupola je opa­sana s pet željeznih prstenova, a kasnije je dodan još jedan.

Na Papinu želju, radio je također na regulaciji rijeke Tiber u Rimu, a zatim na mjerenju meridijanskog luka u Papinoj državi. Za isti posao bio je određen da ide u Brazil, ali na Papin nagovor izvršio je to u Italiji.

Po prvi i posljednji puta nakon odlaska na studij posjetio je svoj rodni zavičaj Dubrovnik 1747. Iz pisama bratu Bartolu i sestri Anici se vidi, da je namjeravao provesti starost u tom gradu. Međutim, prilike nad kojima nije imao kontrolu, skrenule su njegov životni put u drugom pravcu i njegov san nije bio ostvaren.

U to doba, otprilike, počinje i njegova diplomatska djelatnost. Tih godina Dubrovačka republika bila je u velikoj neprilici. Iz Carigrada je, naime, bilo javljeno u, London, da se u Gružu (danas predgrađu Dub­rovnika) gradi ratni brod, koji bi se trebao priključiti francuskoj ratnoj floti pod zastavom Dubrovačke republike. U to doba bili su anglo-francuski odnosi vrlo napeti. Bojeći se engleske odmazde nad njenom trgovačkom flotom, Dubrovačka republika se obratila za posredovanje Boškoviću, svom tada već proslavljenom i poznatom građaninu. Bošković je bio počašćen i ponosan tom ponudom, ali, nažalost, nije bio u mogućnosti da je prihvati i izvede. Kao vještak u isušivanju močvara, bio je poslan po drugoj diplomatskoj misiji u republiku Lucca, da riješi dugo­godišnji spor između nje i Toscane, zbog navodnjavanja i potapanja izvjesnih spornih predjela. Dubrovački problem riješio je papinski nun­cij u Parizu na obostrano zadovoljstvo. Godine 1757. Bošković se uputio u Beč, gdje je riješio spomenuti spor u korist republike Lucca, koja mu ie za nagradu ponudila plemićku titulu; to je on, kao redovnik vezan na poniznost, uljudno odklonio. Na molbu kraljice Marije Terezije ispi­tivao je i podnio izvještaj kako spriječiti i popraviti već nastalo ošteće­nje Carske knjižnice kao i milanske katedrale.

Međutim, za Boškovića je boravak u Beču bio daleko vredniji od svih tih službenih poslova. Već godinama tiho ali uporno, sazrijevala je u njemu njegova Teorija, njegovo životno djelo, po kojemu je zapravo postao besmrtan. Tu u Beču, našao je dovoljno vremena i mira da je dovrši i objavi. Pokušati to u Rimu, gdje su Kopernikove ideje bile skinute s tzv. Indeksa tek 1757, uglavnom upornim Boškovićevim nasto­janjem, bilo bi i izazovno i opasno. Tako mu je ova prilika boravka u Beču dobro došla ne samo zbog diplomatskih usluga, nego ga dovela i do ove razborite odluke. Njegova savjest i kao svećenika, redovnika i naučenjaka bila je čista. U posveti svoje Teorije bečkom nadbiskupu De Migazziju Bošković kaže, da mu „iznosi jednu stvar sasvim ispravnu i ne nudi mu ništa, što bi bilo strano njegovu svećeničkom pozivu, već što se s njim potpuno poklapa“. ([12], Posvetna poslanica autora, str. X.). Godinama, čak još kao mladić u Dubrovniku, razmišljao je o tim idejama, koje su sad konačno sazrele da ih iznese pred svjetsku naučnu javnost. Bio je uvjeren da je došao do istine, kao i u to, da istina nikada ne može biti u konfliktu s vjerom i njenom pravilnom interpretacijom. Koliko je pošten i nepristran bio njegov stav u tim, za ta vremena, škakljivim pitanjima, vidi se iz njegova pisma bratu Baru iz Pariza 1760. god. On piše: „Najveća šteta što se može učiniti vjeri jest htjeti je vezati uz takove stvari u fizici, za koje veliki dio vjernika smatra da su pogrešne. Jer, tada, oni uvjereni u protivno mogu reći, ta i ta je stvar kriva, dakle vjera je kriva i držim, da se tim putem ovdje uistinu teško našodilo vjeri i još se uvijek škodi.“[7]

Tako se u kolovozu 1758. pojavilo prvo izdanje njegove glasovite THEORIA PHILOSOPHIAE NATURALIS, Reducta ad unicam legem virium in natura esdstentium — „Teorija prirodne filozofije, svedena na jedan jedini zakon sila koje postoje u prirodi“. Bila je to knjiga s idejama, koje su u cijelosti shvaćene i prihvaćene, mada u modificira­nom obliku, tek u 20. stoljeću. Bošković je bio svjestan, da će imati potporu manjine, kao što je to redovno slučaj s revolucionarnim ide­jama. Znao je također, da ga većina neće shvatiti i da će ih biti koji će to smatrati sa stanovišta skolastičke filozofije neprihvatljivim. Vjero­jatno ni sam nije slutio, da je tim djelom otvorio sasvim nove vidike, koji će tek u 20. stoljeću dati poticaja za moderni napredak prirodnih nauka, posebno fizike.

Kad je Teorija konačno objavljena, on je bio već u Rimu. Tu je našao da su se mnoge stvari izmijenile za njegova odsustva. Isusovački red je u pojedinim državama bio u teškim neprilikama, a javno mišljenje u gotovo cijeloj Evropi sve se više okretalo protiv njih. Boškovićeve ideje, izražene u Teoriji, kao i ideje o reformi nastave u Collegium Romanum, bile su presmione i nisu naišle na potrebno razumijevanje i potporu. Moguće iz tih razloga, mada to nije sasvim sigurno, a niti je poznato tko je to prvi predložio, Bošković napušta Rim godine 1759. za dulji niz godina. U to vrijeme on je već imao solidnu znanstvenu repu­taciju u cijeloj Evropi, pa postoji mogućnost, da je poslan od strane Reda, da ublaži oštricu javnog mnijenja protiv isusovaca. Ma što bilo, Bošković se rado i spremno uputio prema Parizu 1759. Koliko je dras­tičan, ali i pošten bio njegov stav prema istini, vidi se iz slijedeće zgodice s ovog puta. U Sensu, jednom od brojnih mjesta, gdje se zaustavljao na putu, pokazala su mu uz druge dragocjenosti katedrale komad Aronovog štapa kao i rebro Izaije proroka. Bošković im je jednostavno predložio da u interesu istine to izbace iz crkve.[8]

Koncem te godine nalazimo Boškovića u Parizu, gdje je, unatoč sve većem revoltu protiv isusovaca, bio dobro primljen i u naučnim krugovima, kao istaknuti učenjak, i književnim krugovima kao pro­finjeni pjesnik. Upoznao se s ondašnjim velikim matematičarima D'Alambertom i Clairautom. Clairauta je Bošković veoma cijenio zbog njegova doprinosa višoj analizi. Ostali su kao dobri prijatelji u trajnoj vezi. Za vrijeme boravka u Parizu izabran je za počasnog člana Ruske akademije znanosti i njegovo se ime pojavljuje uz već poznata imena Bernoullija, Eulera, Voltairea, Delislea i drugih. Tu je također intervenirao u korist svoje Dubrovačke republike u jednoj neugodnoj aferi oko francuskog konzula Lemairea u Dubrovniku, koga je francuska vlada na njegovu intervenciju povukla iz Dubrovnika. Za vrijeme ovog boravka u Parizu, radio je na pripremi drugog izdanja svoje Teorije, koje je ispravljeno tiskano u Veneciji 1763., što mu je još više podiglo ugled i poštovanje. Već od 1748. bio je dopisni član Akademije nauka u Parizu, a sad je imao priliku da prisustvuje govorima i izlaganjima već dobro poznatih akademika. Zanimljivo je ovdje napomenuti njegovu korespondenciju s Voltaireom. U samostanskoj biblioteci Male Braće u Dubrovniku[9] postoji kopija pisma na talijanskom jeziku, za koje se smatra da ga je pisao Voltaire. Datirano je 21. VIII 1746. i iz njega se vidi uloga Boškovića u Arkadiji, najznamenitijoj književnoj akademiji 18. stoljeća u Italiji. Pisano je dotjeranim talijanskim jezikom i iz laskavih riječi Voltairea, usprkos njegovu poznatom antireligioznom osjećanju, vidi se, da je on veoma cijenio Boškovića kao književnika i učenjaka, a isto tako i isusovački red.

Nakon posjeta Parizu, Bošković se uputio u Englesku, kamo je sti­gao u svibnju 1760. Najprije je posjetio Greenwich, gdje je upoznao glasovitog astronoma James Bradleya, kojega je Bošković uvijek visoko cijenio i koji je uživao velik ugled među astronomima Evrope.

Tu je dobio vijest, da je za katedru matematike u Rimu imenovan njegov nasljednik P. Asclepi, koga je Bošković cijenio, ali koji mu nije bio dorastao ni u poznavanju nauke, ni u originalnosti ideja. Bošković je bio 45. profesor koji je držao katedru u Collegium Romanum. Bilo je očito da Kolegij nije imao čovjeka koji bi zamijenio Boškovića.

Posjetio je također Oxford i Cambridge. Činjenica što Bošković nije vladao engleskim jezikom nije smetala, da je bio visoko cijenjen u toj zemlji. Njegova Teorija, mada je imala mali broj čitalaca, uvijek je bila cijenjena u naučnim krugovima u Engleskoj u 18. i 19. stoljeću.

Na preporuku Clairauta, u kojoj ga naziva „najveći matematičar kojim se Italija ponosi“, bio je primljen od predsjednika Royal Society u Londonu, lorda Macclesfielda. Tu se također susreo s Benjaminom Franklinom i prisustvovao njegovim eksperimentima s elektricitetom.

Odmah po dolasku, Bošković se uklopio u rad s poznatim astrono­mima Engleske i nastojao je svim silama, da Engleska poduzme vlastitu ekspediciju za promatranje prolaska Venere ispred Sunca u lipnju 1761. O tom događaju napisao je i raspravu: De proximo Veneris sub sole transitu, prevedenu na engleski.[10] Na sugestiju Royal Society sam se spremao da otputuje u Carigrad da bi promatrao taj povijesni događaj. Za svog boravka u Londonu izdao je također knjigu: De Solis ac Lunae Defectibus - O pomrčinama Sunca i Mjeseca - posvećenu Royal Society.

U lipnju iste godine Bošković je predložen za člana Royal Society. Preporuku su potpisali ondašnji poznati učenjaci Engleske, kao lord Macclesfield, J. Bradley, J. Stuart, Davali, Morton i drugi. Tako je u siječnju 1761. konačno izabran za stalnog člana. Bila je to zaista velika čast i priznanje za ovog skromnog hrvatskog svećenika i redovnika, ali i već priznatog evropskog učenjaka.

U prosincu 1760. Bošković napušta London na putu za Carigrad s ciljem da promatra prolazak Venere ispred Sunca. Nažalost, zbog nepredviđenih zaustavljanja na putu i neprilika skopčanih s tim, nije stigao na vrijeme; a kad je konačno stigao, obolio je na nozi, što ga je zadržalo u Carigradu više od pola godine. Na odlasku iz Carigrada, kad se opraštao od Mramornog mora, napisao je kao pozdrav ovu pjesmu, koja govori za sebe o elegantnosti i klasičnosti njegovog latinskog jezika, kao i njegove pjesničke duše:

Aequoris unda vale! Ramosa coralia, conchae,
anguillaeque agiles, squamigerumque pecus,
Nereides, valeant! Valeat cum Doride Thetys,
non placet ilia, udis quae fluit unda comis.
Nos campi, collesque vocant, divaeque virenti
quae fronde atque ornant flore nitente caput.
Non tamen has nimium mirabimur. Est dea nobis,
quae decorat flores, non petit inde decus.[11]

Inače to je putovanje detaljno opisao u poznatom putopisu na talijanskom jeziku, koji je preveden do sada na pet jezika[12] i koji je cijenjen zbog osobito oštrih i točnih zapažanja političkih i ekonomskih prilika na Balkanu.

Na putu su ga uvijek sretali s poštovanjem i priznanjem kao veli­kog učenjaka. Uvijek se kretao u najvišim krugovima svog Reda, naučenjaka, književnika i diplomata. Zadržavši se neko vrijeme u Varšavi, u Poljskoj, konačno, nakon četiri godine odsustva povratio se u Rim 1763. godine. Usprkos činjenici, da je neraspoloženje prema isusovcima sve više raslo i usprkos očitoj slabosti Rima prema njihovim sve brojnijim neprijateljima, Bošković je uvijek ponosno isticao, da je on član tog reda. Gdje god je to bilo potrebno, branio ga je i riječima i svojom naučnom reputacijom od predrasuda, koje su sve više rasle sve do njegovog ukinuća 1773. od strane pape Klementa XIV.

Kako je bio neumoran i svestran, odmah po povratku počeo je raditi na problemu isušivanja Pontijskih močvara, problemu koji se potezao od cara Augusta, Leonarda da Vincija sve do Boškovića. Njegov prijatelj, matematičar Clairaut, šalje mu ozbiljnu opomenu i savjet: „preuzimate suviše mnogo dužnosti, koje apsorbiraju Vaše vrijeme. Preklinjem Vas, nemojte se prenaprezati i oštećivati svoje zdravlje, koje je dragocjeno nama matematičarima“.[13] Usprkos tomu, nastavio je rad i podnio Papinskoj Državnoj upravi izvještaj: Sopra l'asciugamento delle paludi pontine, koji je poslije poslužio kao baza na daljnjem radu oko isušivanja tih močvara.

Iste godine ponuđena mu je katedra matematike na sveučilištu u Paviji, koju je on rado prihvatio. Prilike na sveučilištu bile su daleko od toga da budu idealne prema Boškovićevom shvaćanju. Biblioteka je bila siromašna, a sveučilište nije imalo opservatorija. Umjesto zastar­jelog načina diktiranja predavanja, Bošković traži da se studentima dadnu odgovarajući priručnici. Opservatorij s modernim instrumentima bio je conditio sine qua non. Na taj način profesori bi mogli posvetiti više vremena istraživačkom radu, umjesto da ga troše na ionako dubio zno diktiranje.

Njegove ideje, moderne čak i za naše vrijeme, nisu naišle na pot­rebno razumijevanje. Ipak, uspio je prodrijeti s idejom gradnje novog opservatorija u gradu Brera, na sjevernom dijelu Milana, gdje su isu­sovci imali svoj Collegium. Bošković je sad uložio u tu gradnju svu svoju energiju i neiscrpivo oduševljenje za taj projekt. Zato je imao i svojih posebnih razloga. Već dulje vremena, on je zamislio i namjera­vao izvesti jedan eksperimenat za određivanje brzine svjetlosti u vodi i usporediti je s brzinom mjerenom u vakuumu. To je mislio izvesti mjerenjem aberacije svjetlosti zvijezda pomoću dvostrukog teleskopa, jednog punjenog vodom, drugog praznog. U tu svrhu on je već bio naručio dvocijevni teleskop, koji je bio u izradi, ali koji nije bio nikada dovršen zbog nerazumijevanja na koje je naišao. Da su Boškovićeve ideje tada bile prihvaćene i da su mu dala potrebna sredstva, sasvim je sigurno, da bi on došao do rezultata od neprocjenjive vrijednosti za prirodne znanosti. To je moglo upraviti fiziku u ispravnom smjeru i skratiti za čitavo stoljeće teške napore i sporo probijanje do ispravnih spoznaja i tumačenja eksperimentalnih činjenica i učestalih teoretskih kontradikcija s njima.

Dolaskom novog rektora P. Venninija u Collegium u Breri, situacija se za Boškovića pogoršala. Vennini nije bio sklon da se tolika sredstva od strane Collegiuma ulažu u tzv. „svjetovne nauke“. Tako je Bošković imao sve manje potpore; ipak snalazio se je kako je znao i mogao. Često je nabavljao potrebne instrumente iz vlastitih sredstava, koja bi dobio za razne diplomatske usluge. U isto vrijeme zdravlje mu se pogor­šavalo. Bolest noge, od koje je patio u Carigradu, pojačala se tako da je morao prekinuti rad za neko vrijeme radi liječenja. Kad je odsjek za primijenjenu matematiku bio prebačen iz Pavije u Milano, Bošković se također preselio tamo, što mu je olakšalo rad na opservatoriju u Breri, čije je vodstvo potpuno preuzeo na sebe i smatrao ga u neku ruku svojim vlasništvom.

Uz sav taj rad i borbu oko namaknuća sredstava, nadošle su i druge teškoće čisto iracionalne naravi. Došao je u sukob sa svojim kole­gom, također članom Reda i suradnikom u opservatoriju, L. Lagrangeom. Vjerojatno da su prenaprezanje i pojačana razdražljivost, a s druge strane i dalmatinski temperament utjecali, da se unatoč protivnim savje­tima dao uvući u sitna strančarenja i unutarnje intrige i zavisti, koje su i inače nerijetka pojava u sličnim okolnostima. Usprkos svemu, on je ipak radio neiscrpivom energijom na gradnji opservatorija, iznalazio metode boljih opservacija i usavršavao instrumente. Tu i u takovim okolnostima proveo je skoro deset godina. Međutim, ti sukobi i razila­ženja u mišljenjima stigli su i do Beča, koji je imao kontrolu nad opser­vatorijem. Za vrijeme ljetnih praznika 1772. Bošković je obaviješten od rektora, da je po nalogu iz Beča razriješen dužnosti upravitelja opser­vatorija. Beč se radije priklonio Lagrangeu, smatrajući ga umjerenijim od Boškovića. Profesorsku službu u Milanu je mogao nastaviti.

Ovaj akt Beča, kao i urota njegovih protivnika, povrijedili su Boškovića toliko, da je odbio da se vrati u Milano te je otišao u Vene­ciju. Situacija se pogoršavala do te mjere, da je konačno 1773. rezignirao. Iste te godine dokinut je i Isusovački red. Bošković se našao i s te strane u teškom položaju. Kako sâm sebe naziva, abat Bošković sad se po treći puta uputio u Pariz, gdje mu je francuska vlada dala položaj direktora u Optique Marine, na kojoj je ostao slijedećih deset godina. Tako je opet sitničavošću, zavišću i neshvaćanjem prigušen jedan genij, koji je bio na putu da revolucionira fiziku i druge prirodne znanosti.

Po dolasku u Pariz, Bošković je opazio da su se prilike u Akade­miji znanosti mnogo izmijenile od njegova posljednjeg boravka. Većina njegovih prijatelja, članova Akademije, bili su već umrli. De Lalande, njegov vjerni prijatelj, predložio je, da mu se dadne puno članstvo u Akademiji, čiji je bio dugogodišnji dopisni član. Međutim, poznati mate matičar D'Alambert to je spriječio. On je bio jedan od rijetkih naučenjaka, koji nisu bili skloni Boškoviću. Istina, D'Alambert je respektirao Boškovića kao naučenjaka, mada su se razilazili u mišljenju s obzirom na oblik Zemlje. Lako je moguće, da je on dijelio predrasude ondašnjeg vremena prema isusovcima, tim više, što je pripadao grupi enciklope­dista na čelu s Diderotom, koja je bila izričito antireligiozno usmjerena. Bošković je također bio u sukobu s Laplaceom u pitanju oblika putanje kometa. Komisija Akademije stala je na stranu Laplacea, što je Boško­vića duboko povrijedilo. Onda je došao u sukob s optičarom Rochonom oko prioriteta otkrića prizmatičnog mikrometra, koji su vjerojatno obo­jica simultano i neovisno jedan od drugog pronašli.

Ipak, sva ta razilaženja i sukobi, kao i njegovo sve slabije zdravlje nisu spriječili njegovu neiscrpivu energiju i volju za rad. Tako je 1785. izdao pet knjiga iz optike i astronomije pod. naslovom: Opera pertinentia ad opticam et astronomiam, s dodatkom kratke astronomije za pomorce.

Sad je Bošković bio već u godinama i zdravlje mu je sve više popuštalo. Zato je zatražio i dobio od francuske vlade plaćeni dopust na dvije godine, da ode u Italiju, gdje mu je klima više prijala. Dopust mu je kasnije produljen za još dvije godine, na intervenciju austrijske vlade, koja ga je trebala za neke geodezijske radove. Nakon još jednog puta u Rim, vraća se u ljeto 1786. u Milano i Breru, gdje_pokazuje sve više znakova umnoga poremećenja. Sestri Anici piše u Dubrovnik 26. kolovoza 1786: „Ja sam zdrav u svemu osim u glavi, koja je oslabila i ne mogu s njom činiti, kako sam prije činio“.[14] Poslije dodaje: „Moj se kraj približava - imam 76 godina i osjećam da slabim. Zbogom“. Sve češće je padao u tešku melankoliju, osjećaj proganjanja, nepovjerenja prema svakome, pa i liječnicima, kao i osjećaj teške depresije. Nakon što je pretrpio neke komplikacije na plućima, konačno se 13. veljače 1787. ugasio život tog velikog hrvatskog naučenjaka, koga se bez pretje­rivanja može staviti uz bok Newtona, Bradleya kao i velikih modernih fizičara.

Ruđerove posljednje časove opisao je njegov tajnik i prijatelj Luigi Tomagnini, a pokop njegov skrbnik de Filippi. „Pun predanosti u svoju sudbinu izdahnuo je svoj neokaljani duh na mojim rukama“, piše Tomagnini Lukši Sorkočeviću, u veljači iste godine. Prema de Filippiju, mrtvo tijelo bilo je preneseno u crkvu sv. Marije Pedone i tu je nakon svečanih zadušnica sahranjeno. Nažalost, sticajem raznih okolnost, njegov grob je pao u zaborav, ali je spomen na tog hrvatskog velikana ipak ostao. U matici umrlih 13. veljače 1787. crkve Santa Maria Pedone u Milanu stoji: „Abat, don Josip Ruđer Bošković, Dubrovčanin, profesor matema­tike, 75, peripneumonia“. Slijedi opis posljednjih časova i sahrane u istoj crkvi.

Gilberto Borromeo, član obitelji Borromeo, s kojom je Bošković bio posebno blizak, podigao mu je spomenik s natpisom: „U palači svojih pređa spomenik velikom mužu preminulom u tuđini, radi čašćenja vrli­ne«.[15] U panteonu milanskog groblja istoji ploča s njegovim imenom i godinama 1711-1787. Ovo su interesantni podaci u vezi s njegovim po­rijeklom i nacionalnom pripadnošću: mada je skoro cijeli život proveo u Italiji i tu umro, ipak su upotrijebljene riječi „Dubrovčanin“ i „u tuđini“.

Boškovićeva smrt ocijenjena je u znanstvenim krugovima Evrope, posebno u Dubrovačkoj republici, kao veliki gubitak za nauku. Kome­morirali su je u Francuskoj akademiji, u Milanu i Dubrovniku. Za svoju rodnu grudu Bošković je uvijek imao duboki osjećaj, a brojna pisma braći Boži i Baru kao i sestri Anici ukazuju na to, da je savršeno vladao hrvatskim jezikom, da mu je to bio materinji jezik, koji nikada nije zaboravio, mada je čitav život proveo izvan domovine. U komemoraciji, održanoj u Dubrovniku iste godine, njegov učenik i prijatelj B. Zamagna u Oratio in Funere rekao je: „Takova mu je bila ljubav prema otadžbini u svako doba njegova života, kakova je samo mogla biti u građanina vrlog rodoljuba.“[16] Tražeći iskreno, pošteno i neustrašivo istinu u nauci, Bošković je vjerovao da služi Bogu i u toj vjeri i službi potpuno je izgorio.

Domovina mu se zahvalno odužila; veliki i moderni Institut za fizi­ku i druge grane egzaktnih nauka u Zagrebu ponosno nosi ime: Institut Ruđer Bošković. Ispred njega stoji veličanstvena statua izrađena od I. Meštrovića, drugog hrvatskog genija, koja prikazuje Boškovića u dubokoj misaonoj pozi. U poslijeratno vrijeme, 1958. i 1961, u Hrvat­skoj su održana dva internacionalna simpozijuma, na kojima su sudje­lovali i glasoviti nobelovci Heisenberg i Niels Bohr. Peto, dvojezično izdanje njegove Teorije (latinski i hrvatski), izišlo je u Zagrebu 1974, kao komemoracija 200-godišnjice drugog venecijanskog izdanja. U njemu je fotostatski reproduciran latinski tekst toga izdanja iz 1763. Njemački filozof F. Nletzsche ocijenio je Boškovićev doprinos modernoj nauci ovim riječima: „Rad Kopernika i Boškovića bio je najveći trijumf nad osjetilima, koji je ikad polučen na zemlji.“[17]

II.

Svoje nazore o strukturi materije Bošković je opširno izložio u svojoj THEORIA PHILOSOPHIAE NATURALIS. To je bio jedinstven i jedan od najvećih pothvata u povijesti nauke, da se struktura cijelog Svemira svede na jedan jedini zakon sila koje postoje u prirodi. To opsežno djelo podijeljeno je u tri dijela s nekoliko dodataka i nadopuna; u njemu on iznosi najprije svoju strukturalnu teoriju i pobija moguće prigovore protiv nje, a zatim je primjenjuje na mehaniku, fiziku, kemiju i druge grane prirodnih znanosti.

Treba odmah reći da je ovaj grandiozni pokušaj R. Boškovića bio čisto kvalitativne naravi, izveden spekulativnim putem i zasnovan na poznatim empirijskim činjenicama. Bilo bi i nezamislivo pokušati nešto takvog kvantitativnim putem bez pomoći modernih metoda i visoko-brzinskih elektronskih računskih strojeva (high speed electronic computers), koji su danas u upotrebi.

Raniji atomisti, počevši od Demokrita pa do Newtona, shvaćali su atom kao sićušnu tvrdu i nedjeljivu česticu materije. Demokrit (oko god. 430. pr. Kr.) i neki drugi grčki filozofi smatrali su da je cijeli Svemir sastavljen od tih nedjeljivih - atomos - čestica. Oni nisu mogli pružiti nikakav dokaz za to, osim „tako mora biti“ jer dijeleći materiju u sve sitnije dijelove, dolazimo do čestice koju više nije moguće dijeliti.

Međutim, poznati paradoksi grčkog filozofa Zenona (oko 5. stolj. pr. Kr.) ukazivali su na logičke teškoće takvog zaključivanja, jer snagom iste logike - tako mora biti - moglo se ustvrditi sasvim suprotno. Nije se otišlo mnogo naprijed ni uvođenjem Leibnizovih monada, niti Newtonovih tvrdih, neproničnih čestica s mjerljivom kontinuiranom masom.

Boškovićeva Teorija zapravo je prvi pokušaj da se iziđe izvan gra­nica toga tzv. naivnog atomizma i da se dadne logički i empirički prih­vatljiva zamisao onoga što je materija a, preko toga, što je Svemir. Kao prvi korak, Bošković se oslobodio materijalnih atoma. On nije mogao prihvatiti tvrdu, materijalnu česticu s kontinuiranom masom, koja bi, ma kako da je malena, bila nedjeljiva. Bio bi to logički apsurd. Jedini put da ga se zaobiđe bio je odbaciti materijalnu prirodu atoma. Zamisao je za ono doba bila zaista smiona, posebno jer je kvalitativne naravi i mada sadrži i nutarnjih netočnosti, ipak je bila prva koja je ukazala na pravi put k modernom shvaćanju atoma.

Dvije osnovne Boškovićeve ideje koje dominiraju u cijeloj Teoriji jesu:

1) točke (punkta) tvari, koje izgrađuju Svemir i

2) zakon sila, koje djeluju među tim točkama.

Bošković definira svoja punkta ovako: „... osnovni su elementi materije posve nedjeljive i neprotežne točke, koje su u beskrajnom vakuumu tako razasute, da su po dvije bilo koje od njih međusobno udaljene nekim razmakom, koji se može beskonačno povećavati ili sma­njiti, ali nikako ne može posve nestati bez međusobne kompenetracije tih točaka“. (12, br. 7). Pošto ne pripušta mogućnost kompenetracije, tj. da bi dvije točke zauzimale istu točku prostora, on veli na istom mjestu dalje: „Stoga ja ne mogu prihvatiti, da bi vakuum bio rasut u materiji, već smatram, da je materija rasuta u vakuumu i u njemu plovi“.

Bošković prihvaća neke od Newtonovih ideja, posebno one izražene u Optici o uzajamnim silama, privlačnim i odbojnim. Od Leibniza prihvaća „prve i neprotežne elemente“. Također prihvaća njihov princip interakcije čestica u Svemiru, prema kojem svaka promjena gibanja jedne čestice, ma kako ona bila udaljena, utječe na faktore, koji deter­miniraju gibanje drugih čestica. Isto tako on prihvaća i njihovu osnovnu analitičku metodu. Ali on ima i principijelnih razlika s obojicom uče­njaka. Newton u svojoj Optici pokušava svesti prirodne pojave na tri osnovna principa: gravitaciju, koheziju i fermentaciju. Bošković to svodi na jedan jedini zakon sila, koji, djeluje među punktima materije. S druge strane, on ne prihvaća postojanje tzv. pozitivnih, odnosno privlačnih sila u vrlo malim udaljenostima, nego uvodi suprotne, odbojne sile, koje rastu u beskonačnost, što udaljenost među centrima djelovanja, odnosno između njegovih punkta postaje sve manja. Na taj način Bošković isklju­čuje mogućnost tzv. matematičkog dodira materije, a pojavu kohezije tumači kao posljedicu nečeg sasvim različitog od onog što je Newton pretpostavljao. On zabacuje Leibnizovu ideju kontinuirane protežnosti, „koja bi proistjecala iz susljednih neprotežnih točaka, što se međusobno dodiruju“. (12, br. 3). Isto tako zabacuje nehomogenost elemenata, koju Leibniz temelji na principu da „priroda ne trpi sličnosti“. Naprotiv, Bošković suprotstavlja tome načelo jednostavnosti. Kemijskom analizom dolazimo uvijek do sve manjeg broja sastavnih elemenata, kao i do sve manjeg broja različitih principa i „na kraju dolazimo do homogenosti i potpune jednostavnosti“. Razlike koje zapažamo u prirodi dolaze od različitog kombiniranja homogenih elemenata, kao i izvanjskih smetnji, koje uzrokuju formiranje amorfnih masa. U toku slijedećeg stoljeća ovo je načelo potvrđeno od strane Mendeljejeva, Rutheforda i Mosleya, kao i u moderno doba od N. Bohra i drugih atomista, da je naš poznati Svemir sastavljen od jednog počela ili elementa vodika. Kvantna fizika unijela je u Boškovićev model, kao i u druge predložene modele atoma, mnogo značajnih modifikacija, ali načelo homogenosti, koje je Bošković zastupao, ostalo je netaknuto.

Bošković je bio potpuno svjestan da se sa svojim idejama sup­rotstavio dvojici najvećih suvremenih autoriteta na polju prirodnih nau­ka i samo duboko uvjerenje u ispravnost svojih shvaćanja dalo mu je hrabrosti za to.

Druga osnovna ideja Boškovićeve Teorije, usko vezana s ovom, jest zakon sila koje djeluju među točkama materije. Odmah u početku, Bošković se ograđuje od pokušaja da protumači porijeklo tih silä: „ja to ne ispitujem, a i kad bih htio, nemam nade da bih to mogao otkriti“ (12, br. 9). Ovdje se očito vidi, koliko je bio oprezan, da ne bi prelazio iz fizičkog u metafizički, ili čak vrhunaravni red. On jednostavno pret­postavlja njihovu egzistenciju, otkriva njihovu determiniranost i opi­suje njihovo djelovanje.

Kao prvu i veoma važnu stvar, Bošković uspostavlja funkcionalnu vezu između vrijednosti silä koje djeluju između dvije materijalne točke i njihove međusobne udaljenosti, odnosno razmaka. On kaže: „one su pri neznatnim udaljenostima odbojne i povećavaju se beskonačno, kao što se pri udaljenosti beskonačno smanjuju, tako da su kadre uništiti svaku, ma kako veliku brzinu, kojom bi se jedna točka mogla približa­vati drugoj prije negoli iščezne njihova udaljenost... Povećavanjem udaljenosti sile se smanjuju, nestaju, zatim prelaze u privlačne, koje najprije rastu, zatim padaju, iščezavaju, prelazeći u odbojne i rastući na isti način, zatim opadajući, iščezavajući i prelazeći ponovno u privlačne, i tako redom izmjenično na brojnim ali još posve malim udaljenostima, sve dok, nakon što su došle na nešto veće udaljenosti, ne počnu postajati trajno privlačne i približno obrnuto razmjerne kvadratima udaljenosti«.[18] (12, br. 10). U modernoj fizici slična funkcionalna ovisnost naziva se potencijalnom funkcijom.

Svoj zakon sila Bošković ilustrira krivuljom prikazanom na sl. 1. i uspoređuje je s krivuljom, koja proizlazi iz Newtonovog zakona sila, sl. 2.

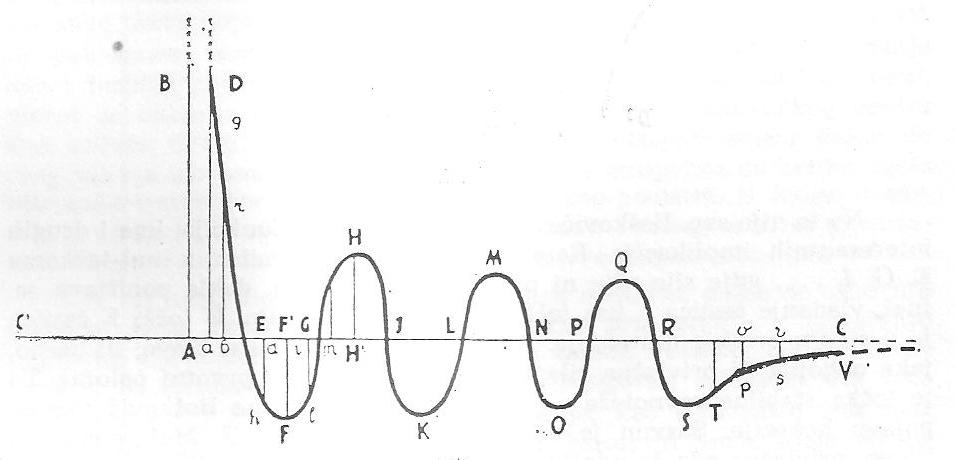
Sl. 1.

Dužina C'C predstavlja os apscisa, na koju se nanose razmaci dviju točaka, (dok ordinate ag, br,..., po,...,) predstavljaju vrijednosti sila. Pozitivne ordinate (npr. br, mn,..., zt,...) predstavljaju odbojnu, a negativne (npr. dh,..., op, .. .) privlačnu silu, koja djeluje među pojedinim točkama.

Treba odmah naglasiti da je Boškoviceva krivulja na sl. 1. bitno kvalitativne naravi. Funkcija, koju ona predstavlja, visoko je fleksibilna i u svom algebarskom obliku, ma kakav on bio, pripušta veliki broj parametara. Na taj način broj presjecišta s osi C'C, odn. nul-točke sila, mogu po volji varirati, kao i visina i širina samih lukova. Označimo li udaljenost dviju točaka u danom času sa r, tada vidimo, da je za udalje­nost r ⁼ Aa sila među česticama pozitivna, tj. odbojna i jednaka visini ordinate ag. Ako r ®  0, tj. ako se čestice približavaju jedna drugoj po volji blizu, tada luk ED, koji opisuje veličinu sila, naglo raste i asimptotski se približava pravcu AB, što znači da ga siječe u beskonačnosti. Drugim riječima, ako razmak među česticama postane po volji malen (infinitezimalan), odbojna sila među njima raste preko svake mjere, što objašnjava svojstvo neproničnosti tvari, a još više činjenicu, da dvije točke materije (punkta), bez obzira na to što su one, ne mogu nikada koincidirati. U modernoj fizici to se područje naziva područje visoko energetske interakcije (high energy interactions). Usporedimo li sl. 1. i sl. 2, koja prikazuje Newtonov zakon sila, odmah je jasno, da tu postoje samo privlačne sile i ako r ®  0, cijela materija bi se srušila u sebe. Kod Boškovića je Newtonova gravitacija samo specijalni slučaj njegova zakona sila kad r ®  ∞, a prikazana je na sl. 1. lukom RSV.

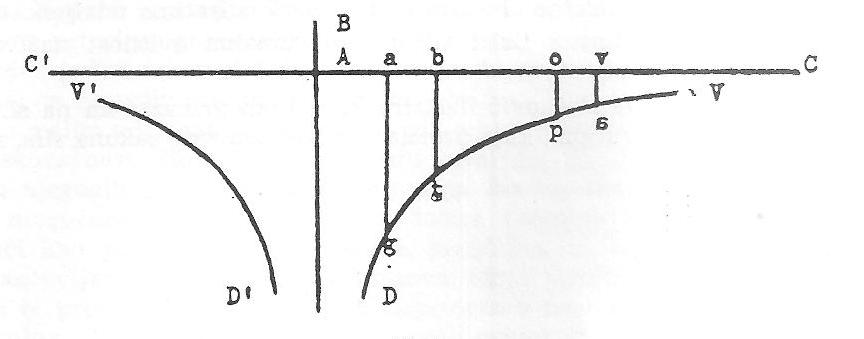
Sl. 2.

No to nije sve. Boškovićeva krivulja, odnosno funkcija, ima i drugih interesantnih implikacija. Razmotrimo vladanje čestica u nul-točkama E, G, I, ..., gdje sila nije ni privlačna ni odbojna, dakle poništava se. Ipak vladanje čestica u tim točkama je bitno različito. U točki E čestica je u stanju čvrstog mirovanja. Ako se malo pomakne u lijevo, ili desno, jaka odbojna ili privlačna sila vratit će je natrag u prvotni položaj. To je točka stabilne ravnoteže - limes cohaesionis, čime Bošković tumači pojavu kohezije. Sasvim je druga situacija u točki G. Mali pomak u lijevo, privlačna sila će udaljiti česticu od te točke, kao što će to učiniti i odbojna sila kod malog pomaka čestice u desno, samo u suprotnom smjeru. To je točka labilne ravnoteže- limes non-cohaesionis, kako je on naziva. Općenito u području luka odbojne sile npr. GHI čestice će se približavati jedna drugoj u jednom smjeru, dok će se u području luka privlačne sile, npr. EFG, čestice približavati jedna drugoj u sup­rotnom smjeru od onog prvog. Ako je, dakle, polje sila unutar tih lukova dovoljno jako, gibanje može rezultirati u oscilatorno.

Ako bismo poznavali realnu, ili bar približno realnu, vrijednost ovakove funkcije, Bošković ustvari tvrdi, da bi to bilo dovoljno, da se izvedu sva svojstva neke tvari ili elementa. Da je njegova tvrdnja bila točna, potvrđeno je tek u moderno doba, kad je upotrebom visoko brzinskih elektronskih računara (high speed electronic computers) konstruiran niz ovakovih realističkih funkcija i kad je pokazano, da baš ovakove visoko fleksibilne funkcije daju potencijale blize pravim vrijednosti­ma.[19]^,[20]^,[21] Također 200 godina nakon Boškovićeve Teorije, po prvi puta su, iz predloženih modela potencijalne funkcije, izvedena sva svojstva ple­menitih plinova argona, kriptona i ksenona[22]^,[23]^,[24].

Bošković je pronašao svoju Teoriju proučavajući zakon kontinuiteta i zakon impulza. On definitivno prihvaća ideju Leibnizove škole, „nihil in natura per saltum fieri“, ali i detaljno proučava one pojave koje na prvi pogled izgledaju da ruše taj zakon. Tipičan primjer za to, koji on detaljno diskutira, jest sraz masa različitih brzina, bilo da se gibaju u istom ili suprotnom pravcu. Naoko, to je diskontinuirana pojava, gdje se brzine masa trenutačno, bez ikakovih prijelaznih faza mijenjaju. U točki br. 18. svoje Teorije on za to navodi i matematički obrađuje jedan primjer sraza dviju masa koje se gibaju različitim brzinama u istom pravcu. Bošković nije ni slutio, da je točnim i detaljnim opisom tog sraza ocrtao pojavu kojom se bavi jedna od najnovijih grana moderne matematike - Catastrophe Theory - matematička metoda, koja prou­čava diskontinuirane pojave u prirodi i svakidanjem životu.[25] Međutim, ma kako takve pojave izgledale na prvi pogled diskontinuirane, Bošković ih ipak smatra kontinuiranim, dajući za to opširno logičko opravdanje kao i lucidan geometrijski dokaz. (12. Sl. 3). Zadržavši pak taj zakon, morao je ukloniti svaku mogućnost neposrednog, matematičkog dodira kod sudara dvaju tijela. Odatle je logičkim zaključivanjem došao do svog zakona uzajamnih sila, koji ima jednu od posljedica da brzina tijela niti može trenutačno nastati, niti se trenutačno poništiti. S druge strane, te sile moraju pri većim udaljenostima opadati i asimptotski se približa­vati nuli, jer bi inače došlo do raspršenja sveukupne materije.

Na taj način Bošković je kvalitativnom metodom došao do osnovnih postavki svoje Teorije, koju nadalje opširno primjenjuje u tumačenju fizikalnih i kemijskih pojava, kao što su talište, vrelište, temperaturne razlike tih točaka za različite tvari itd. Njegovim zakonom sila lako se objašnjava i kristalna struktura materije, kao i to zašto ista tvar uvijek pokazuje jednaku kristalnu formu. Nasuprot tome, ideja tvrdog sfernog atoma (hard spherical atom) mogla je dati tek objašnjenje amorf­nog stanja materije.

Boškovićeva Teorija nije samo fizikalni i matematički pokušaj tumačenja atomizma, nego sadrži u sebi i koncepcije filozofske naravi, kojima on pokušava tumačiti fizikalnu realnost. Najvažnije od njih jesu slijedeće:

1) Osnovni elementi materije su identične, prostorno neprotežne i nedjeljive točke.

2) Točke materije ne posjeduju masu u klasičnom smislu, ali jer su jezgre sila, one su fizička realnost.

3) Sve fizikalne pojave rezultat su jednog jedinog zakona sila.

4) Ne postoji apsolutni prostor; prostor i vrijeme su relativni.

5) Materija posjeduje pretrgnutu, nekontinuiranu strukturu.

6) Postoje polja sila.

Prvo pitanje koje se ovdje samo od sebe nameće jest, što su to neprotežne, nematerijalne i nedjeljive točke i kako sastaviti neko fizičko, protežno tijelo od njih? Bošković sam odgovara na to pitanje ovako: Zbog zakona sila, odbojnih i privlačnih, točke će se rasporediti u tri dimenzije i biti odvojene jedna od druge konačnim razdaljinama. Takav skup točaka zajedno sa svojim silama proizvodi empiričko svojstvo protežnosti. Fizičko tijelo nije kontinuum, nego konačan skup diskon­tinuiranih točaka. Prema tome, u fizikalnoj realnosti ne može biti diobe ad infinitum, kao u geometriji. Masa tijela određena je brojem tih točaka u danom volumenu.

Bošković je bio svjestan da će ovo teško pitanje, kao i odgovor na njega izazvati mnogo kontroverzija u ondašnjim naučnim krugovima. Ipak, on je ostao čvrsto pri svojoj koncepciji, smatrajući je jedinom lo­gički prihvatljivom. U krajnjoj liniji problem bi se svodio na to da se na­đe zadovoljavajući odgovor na pitanje: što su to subatomske čestice u mo­dernoj atomistici, posebno što je to elektron? S jedne strane, danas je poznato da se subatomske čestice, a isto tako i čisto energetske pojave, kao npr. svjetlost, ponašaju i kao čestica i kao čisto valno gibanje; obje fizikalne realnosti imaju, dakle bitno dualnu prirodu. To je duboko i unutarnje svojstvo materije. S druge strane, prema kvantnoj mehanici, oscilatorni sistem posjeduje tzv. nul-energiju (zero-point energy) ili ener­giju mirovanja. Ona je u krajnjoj liniji povezana s Heisenbergovim principom neodređenosti (uncertainty principle): subatomska čestica se ne može specificirati u mirovanju. Ova osnovna energija prestavlja ener­giju fluktuacija, koje se neminovno događaju unutar materije i koje u zakone kvantne mehanike unose statističku prirodu, čak ako se radi i o samo jednoj čestici. To je jedan od osnovnih principa kvantne meha­nike, koji čini gornje pitanje još težim, a možda i beznadnim za odgovor. Filozofski, to je zaista neprijatna spoznaja i jedino što je utješno u njoj jest, da smo u stanju spoznati granice naše spoznaje.

Važno je primijetiti što o tome problemu misli Max Planck, osnivač moderne teorije kvanta. Na jednom mjestu on veli: „Und so sage ich nach meinen Erforschungen des Atoms folgendes: Es gibt keine Materie an sich. Alle Materie entsteht und besteht nur durch eine Kraft, welche die Atomteilchen in Schwingung bringt und sie zum winzingsten Sonnen­system des Atoms zusammenhält“.[26]

Nesumnjivo je da Boškoviću pripada zasluga, što je skoro 200 godina prije atomske ere logički postulirao postojanje neprotežnih i nedjeljivih točaka i time započeo jedan koncept od osnovne važnosti za modernu nauku te, kako se o njemu izrazio nobelovac Heisenberg, „prvi dao ključ za razumijevanje strukture materije“.[27]

Bošković definitivno zabacuje Newtonovu ideju apsolutnog pros­tora kao čisti ens rationis, čija egzistencija nema nikakvog fizikalnog opravdanja. Nasuprot tomu, Bošković suprotstavlja dva prostora: imagi­narni, i fizički, ili realni prostor. Prvi prostor je metafizičkog značaja; to je geometrijski, neprekidan i beskrajno djeljiv prostor. Fizički prostor je onaj, koji ne postoji bez materijalnih objekata.

Boškovićev imaginarni prostor izazvao je dosta kontroverzija i u ondašnje i u moderno doba.[28] Sâm Bošković nije sasvim jasan u tome, jer u uvodu svoje rasprave „O djeljivosti materije“ kaže: „Mada je čisto imaginaran, ipak nije čisto ništa“.[29] On uvodi i tzv. zvjezdani prostor, tj. prostor u kome se gibaju sva nebeska tijela pristupačna našim opa­žanjima. Zvjezdani prostor, prema Boškoviću, smješten je u taj imagi­narni prostor i u njemu se giba. Na taj način, čini se, kao da se Bošković ipak povratio na ideju apsolutnog prostora, tako da bi ova stvar trebala definitivne dublje analize, da bi se vidjelo što je on zapravo podrazumijevao pod tim konceptom.

U Dopuni I. svoje Teorije Bošković opširno raspravlja o prostoru i vremenu. On definira dva načina ili „moda“ postojanja, mjesni i vre­menski. Svaka njegova točka ima realne mode egzistencije, „od kojih se jedni odnose na mjesto, a drugi na vrijeme. Prvi su lokalni, a drugi vremenski. Svaka točka ima stvarno jedan način postojanja, po kojem se nalazi tamo gdje jest, i drugi po kojem se nalazi u vrijeme kada postoji“. (12, Dop. I, br. 4). To su mjesne i vremenske točke. Skup mjesnih točaka sačinjava „realni prostor“, koji se proteže u tri dimenzije, a skup vremenskih „realno vrijeme“, koje ima samo jednu dimen­ziju, trajanje. Prema tome, realnost prostora i vremena vezane su uz egzistenciju tih prostornih i vremenskih točaka. Odatle nužno proizlazi relativnost gibanja, kao prostorno-vremenskog fenomena.

Vrijedno je spomenuti, da je Bošković uvođenjem prostornih i vremenskih moda egzistencije realnih točaka materije došao do ideje Lorenzove kontrakcije dužina pri gibanju, kojom je Lorenz pokušao tumačiti negativni rezultat Michelsonova pokusa, kao i konstantnost brzine svjetlosti, koja je odatle rezultirala. Za Boškovića, razmak između dviju točaka nije nužno isti nakon translacije jednostavno zbog toga, što njihovi prostorni modi nisu više nužno isti. To isto vrijedi i za vremenske događaje. Tako je Bošković kojih 150 godina prije Einsteina došao do koncepcija, iz kojih je nikla njegova glasovita teorija relativiteta. Zato bez pretjerivanja možemo reći da je Bošković bio preteča Einsteina i moderne teorije relativiteta.

Utjecaj Boškovićevih ideja na fizičare 19. stoljeća bio je nesum­njivo dubok, kako to sâm nobelovac Niels Bohr priznaje.[30] L. Pearce Williams daje značajne detalje o tome na koji su način Boškovićeve ideje utjecale na M. Faradaya[31] kod tumačenja induktivnih i elektrolitskih pojava, a preko njega i na J. C. Maxwella kod proučavanja pojava, koje su dovele do otkrića elektromagnetskih valova. Maxwell misli, „da najbolja stvar koja se može postići jest riješiti se krute jezgre i zami­jeniti je Boškovićevim atomom.[32] Boškovićeva koncepcija atoma bila je Faradayu prihvatljivija od one, koju je pružala naivna atomistika onoga doba. On sam kaže: „da izgleda, da je najsigurniji put postulirati što je moguće manje, a to je upravo i razlog, zbog koga mi se čini, da Boškovićevi atomi imaju veliku prednost nad uobičajenim shvaćanjem“.[33] Na taj način, za Faradaya, atomi se pojavljuju u obliku sila, a atmosfera oko središta tih sila (dakle, oko punkta) daje im svojstvo stvarnosti. Usvajajući tu sliku atoma, Faraday je lakše savladao mnoge teškoće ü shvaćanju električne provodljivosti i indukcije. S punim pra­vom, dakle, možemo Boškovića smatrati pretečom moderne teorije polja.

Na kraju dodajmo i ovo. U njegovo vrijeme bilo je vrlo teško, ako ne i nemoguće, pomiriti nauk Crkve o nepomičnosti Zemlje (rezultat pogrešnog tumačenja Sv. pisma) s dostignućima Kopernikove, Galilejeve i Keplerove astronomije. Mnogi, mada uvjereni u protivno, jednostavno su izjavljivali poslušnost službenom naučavanju Crkve. Bošković, među­tim, rješava tu dilemu dubljim razmatranjem, nastojeći pomiriti nauk Crkve i dostignuća moderne astronomije. Uvodeći tzv. „zvjezdani pro­stor“, on misli, da bi Zemlja bila u mirovanju za promatrača izvan toga prostora, dočim bi se gibala za promatrača unutar tog prostora. Za to navodi primjer mrava, koji se giba po obodu kotača istom brzinom, ali u suprotnom pravcu nego kotač. Za promatrača izvan tog sistema mrav bi bio u mirovanju, dočim za promatrača unutar sistema kotača, bio bi u gibanju. (O plimi i oseci).

***

Nema sumnje da je Bošković posjedovao vanrednu stvaralačku fan­taziju, spojenu s dubokom znanstvenom intuicijom, kao i težnjom, da unese logičke i racionalne elemente u sve svoje koncepcije, koje nije bio u stanju provjeriti kvantitavnim putem. Zbog toga je potreban oprez i kritičnost u proučavanju i primjeni njegovih ideja; ma kako one izgledale ili zaista bile genijalne, bio je to samo početak i prvi korak u tamu nepoznatog. Ipak, njegov zakon sila ostaje trajno lijep primjer znanstvene sinteze, koja je pokazala, da intermolekularne sile, ili intermolekularna energija, zaista determinira sva svojstva dane stvari, kao i to, da se ta potencijalna energija, bar približno i u principu može proračunati. Stoga možemo bez pretjerivanja ustvrditi da je Ruđer Boš­ković bio najveći hrvatski mislilac prirodne filozofije, koji je „duboko zaronio u ocean strukture tvari, i da ga rezultati današnje nauke o sastavu tvari ne bi iznenadili drugim, doli mnoštvom, novošću i pre­ciznošću“.

BIBLIOGRAFIJA

F. Rački, Ruđer Josip Bošković, Životopisna crta, Rad JA, 1887, 88—90.

V. Varićak, Matematički rad Boškovićev, Rad JA, 1910, 181, 75—208.

V. Varićak, Ulomak Boškovićeve korespondencije, ibid. 1911, 185, 243—453.

V. Varićak, Prilozi za biografiju Ruđera Boškovića, Rad JA 1926, 232,

V. Radatović, Nekoliko hrvatskih pisama Boškovića sestri Anici, ibid, 75—91.

V. Varićak, Nekoliko pisama Boškovićevih, Rad JA, 1931, 241, 207—228.

J. Zovko, Boškovići u selu Orahovi Dol, Vrela i prinosi, 1938, 8, 74—82.

Građa za život i rad Ruđera Boškovića, Rad JA, 1950, 1958.

Ž. Marković, Almanah Bošković, 1950, 137—191.

M. Scully, A great but forgotten Jesuit scientist, R. J. B. Modern Humanist, Weston, Mass.

L. Whyte, Roger Joseph Boscovich and the Mathematics of Atomism, Notes and Records of the Royal Soc, 13, 38, 1958.

The World of Atom, Basic Bocks, 1976, I, 8/ 117—128.

Mme. Natalie Georgievitch, Zapisi o R. J. Boškoviću, 1932., Samostan Male Braće, Dubrovnik.

Matica Umrlih crkve Santa Maria Pedone, Milano.

[1] MENDELJEJEV: Osnovi kemije, London, 1905.

[2] A Theory of Natural Pholosophy, by R. J. Boscovich. Latin-English Ed., 1922., Open Court, London. Tvrdnja Petronijevića, da je porodica Boškovića čisto srpskog porijekla („of purely Serbian origin“) nije ničim dokazana, pa bi bilo interesantno saznati na temelju čega je Petronijević došao do tog zaključka. Mi ćemo se u daljnjem tekstu studije osvrnuti na njegovo porijeklo. Inače, Boškovića su svojatali i drugi. Pošto je veći dio života proveo van domovine, uglavnom u Italiji i Francuskoj, neki ga nazivaju Talijanom, a drugi Francuzom.

[3] J. J. DE LALANDE: Eloge, Paris 1787.

[4] L. L. WHYTE, Editorial Note for R. J. Boscovich, New York, 1961.

[5] Ž. MARKOVIĆ: Ruđer Bošković, Zagreb 1968.

[6] Marin Getaldić, 1566.1628. Glavno djelo: De Resolutione Mathematica. Smatra se prethodnikom Descartesa.

[7] R. J. BOŠKOVIĆ: De Solis ac Lunae Defectibus, 1735.

[8] E. HILL: Roger Boscovich, A Bibliographical Essay, New York 1961.

[9] Mme. NATALIE GEORGIEVITCH, Zapisi o R. J. Boškoviću, 1932.

[10] R. J. BOSCOVICH: On the next approach of the transit of Venus over the Sun, Royal Soc. Phil. Trans., Vol. XI, 1760.

[11]

Ostaj zdravo morski vale! Razgranati koralji, školjke
- jegulje vitke, morem nastanjene životinje.
Nerejide, da ste zdravo! Ostaj zbogom, Tetijo s Doridom,
ne sviđa mi se on što plovi valovima s vlažnom kosom.
Mene zovu polja i bregovi, koji kite božici mladoj
glavu lišćem i krasnim cvijećem.
Pa ipak ovima neću se diviti najviše. Imam božicu
koja krasi cvijeće, a odatle ne traži slave.

(Okean i Tetija su muž i žena, Doris je njihova kći, koja se udala za Nereja,  morsko božanstvo u dubinama, koje ima svojstvo pretvaranja u druga bića, ako mu to zatreba. On i Doris imaju djecu, Nerejide, morske vile).

[12] Journal d'un voyage de Constantinople en Pologne, par P. R. J. Boscovich, 1772.

[13] Vidi bilješku 7.

[14] Vidi bilješku 5.

[15] Rad Jug. ak., knj. 87—90, str. 93.

[16] B. ZAMAGNA: Oratio in Funere R. J. B., Ragusa 1787.

[17] F. NIETZSCHE: Jenseits von Gut und Böse, 1895.

[18] JOSIP RUĐER BOŠKOVIĆ: Teorija Prirodne Filozofije, Zagreb, 1974.

[19] J. A. BARKER: Interatomic Potentials lor Inter Gases from experimental data, in „Rare Gas Solids“, Ch. 4, Acad. Press, 1975.

[20] J. A. BARKER, R. A. Ficher, R. O. Wats, Mol. Phys. 21, 657, 1971.

[21] J. A. BARKER, R. O. Wats, Jong K. Lee, T. P< Schafer and Y. T. Lee, J. Ch. Phys. 61, 3081, 1974.

[22] M. V. BOBETIĆ: Ph. D. Thesis, University of Waterloo, Waterloo, Ont. 1971.

[23] M. V. BOBETIĆ, J. A. BARKER, Phys. Rev. B2, 4169, 1970.

[24] M. V. BOBETIĆ, J. A. BARKER, M. L. KLEIN, Phys. Rev. B5, 3185, 1972.

[25] Science, AAAS, 196, 287, 1977.

[26] Paulus Kalender, Paulus Verlag, Freiburg, Switzerland, 1975.

- Na temelju mog istraživanja atoma mogu reći slijedeće: Ne postoji materija u sebi. Sva materija nastaje i postoji preko sile, koja prisiljava atomske čestice na oscilacije i tako ih drži skupa, poput sićušnog sunčanog sistema.

[27] Actes du Symposium International. Dubrovnik 1958., 1961. Zagreb, 1959 , 62.

[28] Rad Jug. Akademije, 87-90, Zagreb, 1887.

[29] R. J. BOŠKOVIĆ: De materiae divisibilitate et et de principiis corporum, Lucca, 1957.

[30] Vidi bilješku 21.

[31] L. PEARCE WILLIAMS, Michael Faraday: A Biography, Basic Books, New York, 1965.; Boscovich and British Chemists, R. J. Boscovich, New York, 1961.

[32] J. C. MAXWELL, Phil. Trans., 49, 157, 1867.; Nature, 16, 246, 1877.

[33] M. FARADAY, Phil. Mag., 24, 1844; Exp. Researches in Electr. I, 544, 1839/55.